အနန္တကိန်းစဉ်တန်းများ (Infinite Series)

13 March 2018

Series ဆိုတာအပိုင်း(term) တွေပေါင်းထားတဲ့ ကိန်းစဉ်တန်းတစ်ခုပဲဖြစ်ပါတယ်။ သင်္ချာပုံစံနဲ့ချုံ့ရေးရင်-

S_N=\sum_{n=0}^N a_n

လို့ရေးပါတယ်။ $a_n$ ဆိုတာ $n$ ကြိမ်မြောက်ကိန်း(term) ပဲဖြစ်ပါတယ်။ $n$ တစ်ခုအတွက် ကိန်းတစ်ခုကိုထုတ်ပေးတဲ့ formula ကိုပေးထားတယ်လို့ယူဆရပါမယ်။ ဥပမာ $a_n=\frac{1}{n^2+1}$ ဆိုသလိုမျိုးပေါ့။ တစ်ခါတစ်ရံမှာ $n$ က 1 ကနေလဲ စတတ်ပါတယ် (ဥပမာ $a_n=\frac{1}{n^2}$ )။

$N$ က finite ဖြစ်ရင် ပေါင်းလဒ်ကလည်း finite ပဲဖြစ်ပါမယ်။ တကယ်လို့ $N \to \infty$ ဆိုရင်ရော။ ကိန်းဂဏန်းတွေကို အနန္တပေါင်းရင် ပေါင်းလဒ်ကအနန္တဖြစ်မလား။ ပေါင်းလဒ်က အနန္တမဟုတ်တဲ့ကိန်းတစ်ခုဆိုရင် ဒီ series က converge ဖြစ်တယ်လို့ခေါ်ပါတယ်။ Convergence ရဲ့ သင်္ချာအဓိပ္ပာယ်ကတော့−

\left| S-S_N \right| < \varepsilon ,\ \text{for} \ N>N(\varepsilon)

$S_N$ က $N$ အရေအတွက် term တွေပေါင်းထားတဲ့ ပေါင်းလဒ်ဖြစ်ပါတယ်။ ဆိုလိုတာက စုစုပေါင်းပေါင်းလဒ်ထဲက သူ့ထက်နည်းတဲ့အရေအတွက် $N$ ကြိမ်ပေါင်းထားတဲ့ ပေါင်းလဒ်ကိုနှုတ်ပြီး ပကတိတန်ဖိုးယူရင် တန်ဖိုးအသေးလေး $\varepsilon$ ထက်ငယ်တဲ့အခါ series က converge ဖြစ်တယ်လို့ဆိုပါတယ်။ ဒီနေရာမှာ $\varepsilon$ ရဲ့တန်ဖိုးက ကြိုက်သလောက်သေးလို့ရတာတောင် သူ့ထက်သေးတဲ့ limit တစ်ခုရှိသေးတယ်လို့ဆိုလိုပါတယ်။

အနန္တကိန်းစဉ်တစ်ခုပေါင်းလဒ်က ဘာလို့အနန္တတန်ဖိုးမရနိုင်တာလဲဆိုတာ ဥပမာတစ်ခုပေးကြည့်ပါမယ်။ သင့်အိမ်မှာ ပါတီလုပ်ဖို့ သူငယ်ချင်းအယောက်အနန္တကို ခေါ်ထားတယ်ဆိုပါတော့။ သင့်ဆီမှာ ပီဇာနှစ်ခုပဲရှိပြီး လာသမျှလူအကုန်လုံးကို ကျွေးရမယ်။ ဒါဆိုသင်နည်းလမ်းတစ်ခုကိုသုံးမယ်။ ဒါကတော့ ဧည့်သည်တွေကို တစ်ယောက်ချင်းဝင်ခိုင်းပြီး နောက်လာတဲ့သူက လက်ရှိကျန်တဲ့ပီဇာရဲ့ တစ်ဝက်ကိုရမယ်။ ဒါဆို ပထမဆုံးလူက ပီဇာတစ်ချပ်၊ ဒုတိယလူက ပီဇာတစ်ဝက်၊ တတိယလူက လေးပုံတစ်ပုံ၊ နောက်လူက ရှစ်ပုံတစ်ပုံ၊ စသဖြင့်ရမယ်။ ပီဇာစုစုပေါင်းကို $S$ လို့ထားရင်−

S=1+\frac 12+\frac 14+\frac 18+...

S=\sum_0^\infty 2^{-n}

ဒါပေမယ့် ပီဇာစုစုပေါင်းကအစတည်းက နှစ်ခုပဲရှိတဲ့အတွက် $S$ က 2 ကိုမကျော်နိုင်ပါဘူး။ နောက်ပြီး $\infty$ အထိမပေါင်းပဲ term အရေအတွက် N မှာရပ်လိုက်ရင်လည်း 2 ထက်နည်းတဲ့တန်ဖိုးကိုရမှာပါ။ N ကိုအများကြီးယူခြင်းအားဖြင့် N ကြိမ်အထိ term တွေပေါင်းလဒ်နဲ့ 2 ကြားကခြားနားချက်ကို နည်းနိုင်သမျှနည်းအောင်လုပ်လို့ရပါတယ်။ ဒါကိုပေါင်းလဒ်က 2 ရဲ့ limit ကိုချဉ်းကပ်သွားတယ် (converge ဖြစ်တယ်) လို့ပြောပါတယ်။ ဆိုလိုတာက $\varepsilon$ ကိုဘယ်လောက်ပဲသေးအောင်ယူယူ ခြားနားချက်−

S-S_N=\sum_0^\infty 2^{-n} - \sum_0^N 2^{-n}

ရဲ့ တန်ဖိုးက $\varepsilon$ ထက်နည်းနေဦးမှာပါ။

ဒီ S series ကို geometric series လို့ခေါ်တဲ့ နောက် term နဲ့ ရှေ့ term ကိန်းသေအချိုး (r) ရှိတဲ့ ကိန်းစဉ်တန်းတစ်ခုနဲ့ ဖော်ပြနိုင်ပါတယ်။ သဘောကတော့−

S_N=1+r+r^2+r^3+...+r^N

အပေါ်က ပီဇာအတွက် ကိန်းစဉ်တန်းဆိုရင် $r=\frac 12$ ဖြစ်ပါမယ်။ S ကို r နဲ့မြှောက်ရင်-

rS_N=r+r^2+r^3+r^4+...+r^{N+1}

$S_N$ ထဲက $rS_N$ ကိုနှုတ်ရင်−

S_N(1-r)=1-r^{N+1}

S_N=\frac{1-r^{N+1}}{1-r}

S_N=\frac{1}{1-r}-\frac{r^{N+1}}{1-r}

အပေါ်ကညီမျှခြင်းကိုကြည့်ရင် ပထမ term $\frac{1}{1-r}$ က ratio $r=\frac 12$ ပေါ်မှသာမူတည်ပြီး ဒုတိယ term $\frac{r^{N+1}}{1-r}$ ကတော့ term အရေအတွက် N ပေါ်မှာလည်းမူတည်တာတွေ့ရပါတယ်။ ဒါကြောင့် $r<1$ ဖြစ်ပြီ: N က $\infty$ ကိုချဉ်းကပ်သွားရင် $S$ က 2 ကိုချဉ်းကပ်သွားတာကို သိသိသာသာတွေ့နိုင်ပါတယ်။

ဒီပီဇာဥပမာကိုကြည့်ပြီ: ဆက်တိုက်နည်းသွားတဲ့ကိန်းတွေကို အနန္တပေါင်းလဒ်က converge ဖြစ်တယ်လို့ပြောလို့မရပါဘူး။ ကိန်းစဉ်တန်းတွေတိုင်းကိုလည်း geometric series ပုံစံနဲ့ဖော်ပြလို့မရနိုင်ပါဘူး။ အနန္တကိန်းစဉ်တန်းတစ်ခုပေါင်းလဒ်က converge ဖြစ်သလားဆိုတာကို စစ်ဆေးတဲ့နည်းလမ်းတွေကို convergence test တွေလို့ခေါ်ပါတယ်။ အခု convergence test တစ်ချို့ကို လေ့လာကြည့်ရအောင်။ ဒီ test တွေအတွက် နမူနာအနေနဲ့ ယေဘူယျအကျဆုံး series ပုံစံဖြစ်တဲ့

S_N=\sum_{n=0}^N a_n

ကိုကြည့်ပါ။ ဒီ series ရဲ့ $a_n$ တွေက အပေါင်းကိန်းတွေဖြစ်ပြီး n တိုးလာတာနဲ့အမျှ $a_n$ ကနည်းသွားတယ်လို့ ယူဆပါမယ်။

Comparison Test

ပထမနည်းလမ်းကတော့ series နောက်တစ်ခုနဲ့ နှိုင်းယှဉ်ကြည့်တာပါ။ $b_n$ term တွေပါဝင်တဲ့ infinite series တစ်ခုက converge ဖြစ်တယ်ဆိုရင် $a_n \leqslant b_n$ (n အကုန်လုံးအတွက်) ဖြစ်ခဲ့ရင် $a_n$ term တွေနဲ့ ဖွဲ့စည်းထားတဲ့ ကိုယ့် infinite series ကလည်း converge ဖြစ်ပါတယ်တဲ့။ ဘာကြောင့်လဲဆိုတာတော့ ရှင်းပါတယ်။ Converge ဖြစ်တဲ့ series ရဲ့ term တွေအကုန်လုံးထက် ကိုယ့် series ရဲ့ term တွေတန်ဖိုးကနည်းနေရင် ပိုပြီးတော့ converge ဖြစ်နိုင်တာပေါ့။ တစ်ခုရှိတာက $a_n$ ကရှေ့ပိုင်း term တွေမှာ $b_n$ ထက်ကြီးနေရင်တောင်မှ ကြီးနေတဲ့ term တွေပေါင်းလဒ်ကို 0 လို့ထားပြီ: နောက်ပိုင်း term တွေပေါင်းလဒ်က converge ဖြစ်တယ်ဆိုရင် $a_n>b_n$ term တွေပေါင်းလဒ်က finite ဖြစ်တာကြောင့် စုစုပေါင်း ပေါင်းလဒ်ကလည်း finite ဖြစ်တဲ့အတွက် series က converge ဖြစ်ပါတယ်။ ဒါကြောင့် convergence test က finite term တွေရဲ့ ပေါင်းလဒ်ကို စစ်တာမဟုတ်ပဲ $N \to \infty$ ဖြစ်တဲ့အခါမှာ converge ဖြစ်သလားဆိုတာသာ စစ်တာဖြစ်ပါတယ်။

ပြောင်းပြန်အနေနဲ့ $a_n \geqslant b_n \text{(for all n)}$ ဖြစ်ပြီ: $b_n$ series က diverge ဖြစ်ရင် (converge မဖြစ်ရင်) $a_n$ series ကလည်း diverge ဖြစ်ပါတယ်။

ဥပမာတစ်ခုအနေနဲ့ $\sum\_{n=1}^\infty \frac{1}{n^2}$ ကိုအကျယ်ဖြန့်လိုက်ရင်−

1+\frac 14+\frac 19 + \frac {1}{16}+...+ \frac {1}{49}+ \frac {1}{64}+...+ \frac {1}{15^2}+...

အဲ့တာကို သူ့ထက်ပိုကြီးတဲ့ အောက်က series နဲ့ နှိုင်းယှဉ်ကြည့်ပါ။

1+2 \times \frac 12+4 \times \frac{1}{16}+8 \times \frac{1}{64}+...=1+1+\frac 12+\frac 14+\frac 18+...

ဒီ geometric series က converge ဖြစ်တဲ့အတွက် term တွေအကုန်လုံးသူ့ထက်ငယ်တဲ့ မူလ series ကလည်း converge ဖြစ်ပါတယ်။

Ratio test

အောက်က(မ)ညီမျှခြင်းကိုလိုက်နာရင် series က converge ဖြစ်ပါတယ်။

r=\lim _{n \to \infty} \frac{a_{n+1}}{a_n} < 1

ဒီ test ရဲ့ သဘောတရားကတော့ n က $\infty$ ကိုချဉ်းကပ်ခိုင်းပြီး series ရဲ့ နောက်ပိုင်း term တွေကို geometric series အနေနဲ့ယူဆလိုက်တာဖြစ်ပါတယ်။ ရှေ့ပိုင်း term တွေပေါင်းလဒ်ကတော့ finite ဖြစ်တဲ့အတွက် $n \to \infty$ မှာ $r < 1$ ဖြစ်တယ်ဆိုရင် series က converge ဖြစ်ပါတယ်။ မဟုတ်ရင်တော့ diverge ဖြစ်ပါတယ်။ $r=1$ ဆိုရင်တော့ အတိအကျပြောဖို့ခက်ပါတယ်။

ဥပမာ ၂.

S =\sum_{n=1}^\infty \frac{n}{3^n}

ဒီပုစ္ဆာမှာ $a_n=\frac{n}{3^n}$ ဖြစ်ပါတယ်။ ဒီတော့

a_{n+1}=\frac{n+1}{3^{n+1}}

r=\lim \_{n \to \infty} \frac{n+1}{3n}=\frac 13

နောက်ဆုံးရလဒ်က L'Hôpital's rule ကိုအသုံးပြုထားတာဖြစ်ပါတယ်။ r က 1 ထက်ငယ်တဲ့အတွက် ဒီ series က converge ဖြစ်ပါတယ်။

ဥပမာ ၃.

a_n=\frac 1n

အတွက် ratio test နဲ့ စစ်ကြည့်ရအောင်။

r=\lim \_{n \to \infty} \frac{n}{n+1}=1

r က 1 ဖြစ်တဲ့အတွက် ratio test ကိုသုံးပြီ: convergence ကိုစစ်လို့မရပါဘူး။

Integral test

$\sum\_{n=1}^\infty f(n)$ က တစ်ဖြည်းဖြည်းနည်းသွားတဲ့ term တွေနဲ့ ဖွဲ့စည်းထားတယ်ဆိုရင် $\int^L f(x) dx$ ရဲ့ $L \to \infty$ မှာ converge ဖြစ်၊မဖြစ်ကိုလိုက်ပြီး series ကလည်း အတူတူဖြစ်ပါတယ်။

$\sum\_{n=1}^\infty f(n)$ က အောက်ကပုံအတိုင်း အမြင့် $f(n)$ နဲ့ အကျယ် $1$ ရှိတဲ့ ထောင့်မှန်စတုဂံတွေရဲ့ ဧရိယာပေါင်းလဒ်နဲ့တူညီပါတယ်။ Integral ကလည်း $f(x)$ curve အောက်ကဧရိယာကိုရတာကြောင့် integral က diverge ဖြစ်ရင် series ကလည်း diverge ဖြစ်ပါတယ်။

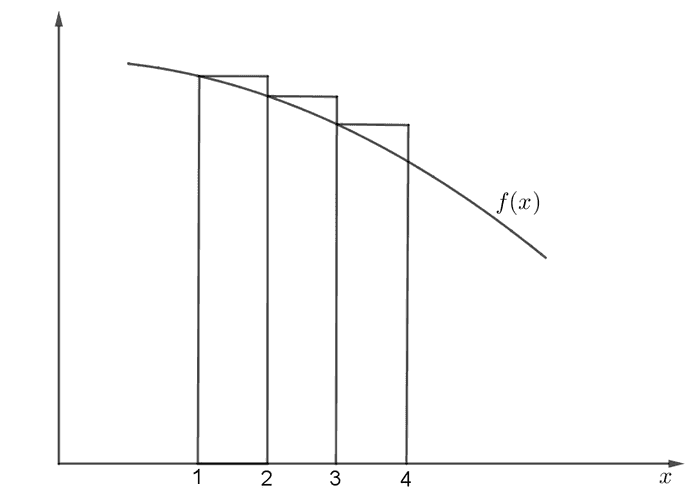
ပုံကိုကြည့်ရင် ထောင့်မှန်စတုဂံဧရိယာက curve အောက်ကဧရိယာထက် နည်းနည်းကြီးနေတာတွေ့ရပါတယ်။ ဒါပေမယ့် $n=1$ နဲ့ $2$ ကြား၊ ရှေ့ဆုံးကထောင့်မှန်စတုဂံတစ်ခုကိုဖျောက်ပြီး နောက်ကထောင့်မှန်စတုဂံတွေကို ရှေ့တစ်ယူနစ်စီတိုးကြည့်ပါ။ ဒါဆိုရင် ထောင့်မှန်စတုဂံဧရိယာတွေက curve အောက်ကဧရိယာထက်ပိုနည်းသွားပါလိမ့်မယ်။ ပထမဆုံးစတုဂံဧရိယာက finite တန်ဖိုးဖြစ်တဲ့အတွက် series ရဲ့ converge/diverge ဖြစ်ခြင်းကို မထိခိုက်စေနိုင်ပါဘူး။

ဥပမာ ၄.

$a_n=\frac 1n$ အတွက်−

\int^L \frac 1x dx \to \infty \ \text{ as } L \to \infty

ဒါကြောင့် $\sum\_{n=1}^\infty \frac 1n$ က diverge ဖြစ်ပါတယ်။

ဥပမာ ၅.

$a_n=\frac {1}{n^2}$ အတွက်−

\int ^L \frac {1}{x^2} dx \approx \frac 1L \ \text{ as } L \to \infty

ဒါကြောင့် $\sum\_{n=1}^\infty \frac 1n$ က diverge ဖြစ်ပါတယ်။

Power series

အပေါ်က series တွေမှာပါတဲ့ term $a_n$ တွေက $n$ ပေါ်မှာသာ မူတည်ခဲ့ပါတယ်။ အခု variable $x$ ကိုထည့်ပြီး ပီဇာဥပမာလိုမျိုး power series တွေကိုလေ့လာကြည့်ပါမယ်။ Power series ရဲ့ ပုံစံကတော့−

S(x)=\sum\_{n=0}^\infty a_n x^n

အရှေ့ကပြောခဲ့တဲ့ series တွေက $x=1$ နဲ့ဖွဲ့စည်းထားတယ်လို့ယူဆနိုင်ပါတယ်။ ဒီနေရာမှာတော့ $x$ တန်ဖိုးကိုမူတည်ပြီ:တော့ series က converge/diverge ကွဲပြားသွားနိုင်ပါတယ်။ ဒီတော့ ပီဇာဥပမာမှာလိုပဲ နောက် term နဲ့ ရှေ့ term ရဲ့ ratio ကိုရှာကြည့်ပါမယ်။

\begin{aligned} r(x) &= \lim _{n\to \infty} \left| \frac{a_{n+1}x^{n+1}}{a_n x_n} \right| \\ &= |x| \lim _{n\to \infty} \left| \frac{a_{n+1}}{a_n} \right| \\ & \equiv |x| \ r \end{aligned}

$r(x)$ က 1 ထက်ငယ်ရင် series က converge ဖြစ်ပါလိမ့်မယ်။

r(x)=|x|r < 1 \\ |x|<\frac 1r \\ |x|<\lim _{n \to \infty} \left| \frac{a_n}{a_{n+1}} \right|=R

R ကို interval of convergence လို့ခေါ်ပြီး $-R<x<R$ ကြားမှာ series က converge ဖြစ်တယ်လို့ ဆိုလိုပါတယ်။

ဥပမာ ၆.

Exponential series အတွက် power series ကိုကြည့်ပါ။

e^x=\sum\_{n=0}^\infty \frac{x^n}{n!}

သူ့ရဲ့ interval of converge ကိုရှာကြည့်ရအောင်။

R=\lim _{n \to infty} \left| \frac{(n+1)!}{n!} \right| = \lim _{n \to \infty} n+1=\infty

ဖြစ်တဲ့အတွက် $x$ က $-\infty$ နဲ့ $+\infty$ ကြား၊ တစ်နည်းအားဖြင့် $x$ တန်ဖိုးအကုန်လုံးအတွက် converge ဖြစ်ပါတယ်။ sin, cos လိုမျိုး trigonometric function တွေနဲ့ sinh, cosh လိုမျိုး hyperbolic function တွေအတွက်လည်း အလားတူပါပဲ။ ဘာလို့လဲဆိုတော့ အဲ့ဒီ့ function တွေကိုလည်း exponential function ကိုပေါင်းစပ်ပြီး ဖော်ပြနိုင်လို့ပဲဖြစ်ပါတယ်။

ဥပမာ ၇.

\frac{1}{1-x}=1+x+x^2+x^3+...

ဒီ series အတွက် $R=1$ ဖြစ်တဲ့အတွက် $|x|<1$ ဖြစ်မှသာ series က converge ဖြစ်မှာဖြစ်ပါတယ်။ $x>1$ မှာ function တန်ဖိုးတွေရှိပေမယ့် ဒီ series နဲ့ဖော်ပြလို့မရနိုင်ပါဘူး။

Convergent infinite series တွေရဲ့ ဂုဏ်သတ္တိတွေကို ဆက်လက်ဖော်ပြသွားမှာဖြစ်ပါတယ်။