ခေတ်သစ်သိပ္ပံမွေးဖွားခြင်း

9 July 2019

mechanics quantum theory statistical mechanics thermodynamics

၁၉ ရာစုနှောင်းပိုင်း သိပ္ပံအနေအထား

၁၉ ရာစုနှောင်းပိုင်းတွင် သိပ္ပံပညာရှင်များသည် ရုပ်ဝတ္ထုရွေ့လျားမှုများကိုအခြေခံသော သိပ္ပံဥပဒေသများက သဘာဝဓမ္မများကို အခြေခံကျကျအမှန်တကယ်ရှင်းပြနိုင်ခြင်းရှိမရှိ မေးခွန်းထုတ်လာကြသည်။ လွန်ခဲ့သောနှစ်တစ်ရာကျော်ခန့်က အိုက်ဇက်နယူတန်ဖော်ထုတ်ခဲ့သော မက်ကင်းနစ်ညီမျှခြင်းများသည် ထိုအချိန်တိုင်အောင် အလွန်အောင်မြင်ခဲ့ပြီး လက်တွေ့စမ်းသပ်ချက်များဖြင့်လည်းကိုက်ညီလျှက်ရှိသည်။ သို့သော် သိပ္ပံပညာရှင်တို့၏ ပင်ကိုယ်စူးစမ်းလိုစိတ်အရ ထိုမက်ကင်းနစ်ဥပဒေသများသည် ရှိရှိသမျှသောသဘာဝတရားအားလုံးကို အကျုံးဝင်ခြင်းရှိ၊မရှိ ဆွေးနွေးကြသည်။ မိုက်ကယ်ဆန်−မော်လီစမ်းသပ်ချက်ကိုပြုလုပ်ခဲ့သော သိပ္ပံပညာရှင် မိုက်ကယ်ဆန် (Michaelson) ကမူ အခြေခံဥပဒေသအားလုံးနီးပါးကို ရှာဖွေတွေ့ရှိပြီးဖြစ်၍ ပိုပြီ:တိကျသောစမ်းသပ်ချက်များကို လုပ်ဆောင်ပြီး ဆက်လက်အသုံးချရန်သာကျန်တော့သည်ဟု ဆိုခဲ့သည်။ မက်စ်ပလန့်၏ဆရာဖြစ်သော ဗွန်ဂျိုလီ (Von Jolly) ကလည်း သိပ္ပံသီအိုရီများသည် ပြီးပြည့်စုံလုနီးပါးဖြစ်သည်ဟု အဆိုပြုခဲ့သည်။ သို့သော်လည်း သိပ္ပံပညာရှင်များအတွက် ငြင်းခုန်စရာကိစ္စရပ်များက ကျန်ရှိနေသေးသည်။

ရွေ့လျားမှု

ပန်းသီးကြွေခြင်းမှစ၍ ဂြိုလ်ပတ်လမ်းများအထိ အရာဝတ္ထုများ၏ရွေ့လျားမှုကို သင်္ချာညီမျှခြင်းများဖြင့် စနစ်တကျဖော်ပြနိုင်ခဲ့ပြီဖြစ်သည်။ အားသက်ရောက်မှုနှင့် မူလအခြေအနေတို့ကိုသာသိရှိပါက စကြဝဋ္ဌာတစ်ခွင်ရှိဝတ္ထုအားလုံးတို့၏ ရွေ့လျားမှုကိုသီအိုရီဖြင့်တွက်နိုင်မည်ဟုအထင်ရှိကြသည်။
မက်ကင်းနစ်ဥပဒေသများက မရှင်းပြနိုင်သော အပူ၊ အလင်းနှင့် လျှပ်စစ်သံလိုက်တို့အကြောင်းကို မက်စ်ဝဲ၏ ကျော်ကြားသော ညီမျှခြင်းများက ဖြေရှင်းနိုင်ခဲ့သည်။ မက်စ်ဝဲညီမျှခြင်းများသည် တစ်ချိန်ကသီးခြားစီဟုထင်ခဲ့သော လျှပ်စစ်နှင့်သံလိုက်ကို ပေါင်းစည်းပေးခဲ့ပြီး လျှပ်စစ်သံလိုက်စက်ကွင်းများကို ဓာတ်ဆောင်အမှုန် (charged particle) များ၏တုန်ခါမှုကြောင့် ဖြစ်ပေါ်လာသောလှိုင်းများဖြစ်သည်ဟု ရှင်းလင်းခဲ့သည်။ ထိုမျှသာမက လျှပ်စစ်သံလိုက်လှိုင်းများပြန့်နှန့်ပုံနှင့် အလင်းသည်လည်းလျှပ်စစ်သံလိုက်လှိုင်းတစ်မျိုးဖြစ်ကြောင်းကို ဖော်ထုတ်နိုင်ခဲ့သည်။

စွမ်းအင်

၁၈၄၁ ခုနှစ်တွင် အပျော်တမ်းသိပ္ပံပညာရှင်တစ်ဦးဖြစ်သူ ရောဘက်မေယာ (Robert Mayer) သည် စွမ်းအင်တည်မြဲမှုနိယာမအကြောင်းကို စာတမ်းရေးသားခဲ့သည်။ သို့သော်သူ၏ တရားဝင်ပညာရေးလစ်ဟင်းမှုကြောင့် စာတမ်းကိုပစ်ပယ်ခြင်းခံခဲ့ရသည်။ တစ်နှစ်အကြာတွင် အလုပ်၊ စွမ်းအင်နှင့် လူ၏စွမ်းအင်ထုတ်လုပ်မှုအကြောင်းကို ရေးသားခဲ့သေးသည်။ ၁၈၄၇ ခုနှစ်တွင် ဂျာမန်သိပ္ပံပညာရှင်ဟမ်းဟော့ (Helmholtz) သည် စွမ်းအင်တည်မြဲမှုနိယာမကို သာမိုဒိုင်းနမစ်ပထမနိယာမအနေဖြင့် အတိအကျဖော်ပြခဲ့သည်။

အက်တမ်နှင့် သာမိုဒိုင်းနမစ်

Ludwig Boltzmann By Unknown - Uni Frankfurt, Public Domain

Boltzmann ၏ kinetic theory of gases သည် ဓာတ်ငွေ့များ၏ ဂုဏ်သတ္တိနှင့် ဖိအား၊ ထုထည်၊ အပူပြောင်းလဲမှုသဘာဝတို့ကို အက်တမ်များတုန်ခါမှုနှင့် statistical mechanics သဘောတရားကိုအသုံးပြုပြီး တွက်ထုတ်နိုင်ခဲ့သည်။ ထိုမှတစ်ဆင့် အရာဝတ္ထုများအချင်းချင်း အပူနှင့် စွမ်းအင်စီးဆင်းမှုကိုဖော်ပြသော သာမိုဒိုင်းနမစ်နိယာမများကို ကလောဆီးယပ်စ်၊ ရန်ကိုင်းစသည့် ပုဂ္ဂိုလ်များက ဖော်ထုတ်ခဲ့ကြသည်။ လျှပ်စစ်သံလိုက်လှိုင်းများနှင့် ဓာတ်ငွေ့များအကြောင်းကို ရှင်းပြနိုင်ခဲ့သောလည်း ထူးဆန်းသည်မှာ ၁၉ ရာစုအကုန်ပိုင်းအထိ အက်တမ်များတည်ရှိမှုမှာ အဆိုပြုချက်အနေဖြင့်သာရှိသေးသည်။ အက်တမ်များသည် အဓိပ္ပာယ်ဖွင့်ဆိုချက်အရ ဆက်လက်မပိုင်းခြားနိုင်သော အခြေခံအမှုန်များဖြစ်သည်။ အရာဝတ္ထုတိုင်းကို အလွန်သေးငယ်သောအမှုန်များဖြစ်သည့် အက်တမ်များဖြင့်ဖွဲ့စည်းထားခြင်းကို စမ်းသပ်ချက်များရှိသော်လည်း အတိအကျသက်သေပြမှုကို မပြုလုပ်နိုင်သေးပေ။ ထို့ကြောင့်အချို့သိပ္ပံပညာရှင်များက အက်တမ်အနုမာနကို လက်မခံခဲ့ကြပေ။ အက်တမ်များတည်ရှိမှုကိုအခြေခံသော ဓာတ်ငွေ့သီအိုရီ (Kinetic theory of gases) ကိုလည်း လက်ခံသူနည်းပါးခဲ့သည်။ ဝတ္ထုများကို အဆုံးသတ်မရှိ အဆင့်ဆင့်ပိုင်းခြားနိုင်မည်၊ တစ်နည်း ဝတ္ထုသည်အစဉ်မပြတ်ဒြပ်ထု (continuous matter) ဖြစ်သည်ဟုလည်း အချို့ကဆိုခဲ့ကြသည်။ ထိုအယူအဆမမှန်ကြောင်းကို ၂၀ ရာစုအတွင်းမှ စမ်းသပ်ချက်များနှင့် ကွမ်တမ်ဥပဒေသတို့ကသက်သေပြနိုင်ခဲ့သည်။

သာမိုဒိုင်းနမစ်နိယာမများသည် classical ရူပဗေဒအတွက် အရေးပါသောထောက်တိုင်များဖြစ်ခဲ့ကြပြီး ယခုအချိန်အထိများစွာအသုံးပြုနေကြဆဲဖြစ်သည်။ ၁၉ ရာစုအလယ်ပိုင်းမှစတင်ထွက်ပေါ်လာခဲ့သော အက်တမ်များတုန်ခါမှု၊ အပူ၊ စွမ်းအင်၊ အမ်ထရိုပီနှင့် ဖြစ်တန်စွမ်းကျမက်ကင်းနစ်၊ လျှပ်စစ်သံလိုက်လှိုင်း၊ ရောင်ခြည်ထုတ်လွှင့်မှု ရှာဖွေတွေ့ရှိချက်များသည် နောင်လာမည့်သီအိုရီများနှင့် သိပ္ပံပညာရှင်ငယ်များအတွက် ကြီးမားသောလမ်းစများဖြစ်လာခဲ့သည်။

ဝတ္ထုနက်ဖြာထွက်ခြင်း (Black body radiation)

လျှပ်စစ်ဓာတ်ဆောင်အမှုန်များ (charged particles) တုန်ခါမှုကြောင့် ရောင်ခြည်ဖြာထွက်ခြင်း (radiation) ဖြစ်ပေါ်လာကြောင်းသိရသည့်အခါ စွမ်းအင်ပမာဏတစ်ခုအတွင်း မည်သည့်ကြိမ်နှုန်းဖြင့် ပြင်းအားမည်မျှထုတ်လွှတ်သည်ကို ဆန်းစစ်ကြသည်။ ဥပမာမီးသီးတစ်လုံးကို လျှပ်စစ်ဓာတ်အားပေးလိုက်ပါက မီးသီးအတွင်းရှိကြေးနန်းမျှင်အက်တမ်များ (သို့) အီလက်ထရွန်များတုန်ခါကြပြီး ရောင်ခြည်အဖြစ် အလင်းကိုထုတ်လွှတ်ပေးသည်။ ထိုရောင်ခြည်ထုတ်လွှတ်မှုကိုဖော်ပြသော ညီမျှခြင်းများသည် kinetic theory of gases မှ အရွေ့စွမ်းအင်−အပူ ညီမျှခြင်းများနှင့်ဆင်တူသည်။ သို့သော်အလင်း၊ရောင်ခြည်ကိုသယ်ဆောင်သောဖိုတွန် (photon) များသည် ဒြပ်ထုမရှိသောကြောင့် အရွေ့စွမ်းအင်ကို $\frac12 mv^2$ ဖြင့်ဖော်ပြ၍မရပဲ အဟုန် အနေဖြင့်သာဖော်ပြနိုင်သည်။

အက်တမ်၊ အီလက်ထရွန်၊ ဓာတ်ဆောင်အမှုန်တစ်ခုသည် သုညထက်မြင့်သောအပူချိန်တစ်ခုတွင်တည်ရှိပါက တုန်ခါခြင်းဖြင့်ရောင်ခြည်ကိုထုတ်လွှတ်ပြီး စွမ်းအင်ကိုဆုံးရှုံးစေသည်။ ထို့ကြောင့်ထင်း၊ မီးသွေးခဲကိုမီးရှို့ထားပါက အပူထွက်လာပြီး သိုလှောင်ဓာတုစွမ်းအင်ကုန်ဆုံးသွားသောအခါ တဖြည်းဖြည်းအေးလာခြင်းဖြစ်သည်။ သို့သော်ထိုတုန်ခါနေသော အီလက်ထရွန်စသည့်အမှုန် (oscillator) များကို ဟင်းလင်းပြင်တွင်မထားပဲအလုံပိတ်အခန်း (cavity) တစ်ခုထဲတွင်ထားရှိမည်။ အခန်း၏နံရံအားလုံးကိုလည်း ရောင်ခြည်ကိုပြန်ကန်ထွက်စေနိုင်သည့် မှန်များတပ်ဆင်ထားမည်ဆိုလျှင် တုန်ခါမှုန်များမှထွက်လာသောရောင်ခြည်များသည် ဆုံးရှုံးသွားခြင်းမရှိပဲ အခန်းအတွင်းတွင်သာ လှည့်ပတ်တည်ရှိနေမည်ဖြစ်သည်။ ထိုရောင်ခြည်များက အခန်းတွင်းရှိတုန်ခါနေသောအက်တမ်များကို ပြန်တိုက်မိသည့်အခါ အက်တမ်များက ရောင်ခြည်စွမ်းအင်တစ်ချို့တစ်ဝက်ကို ပြန်လည်ရရှိမည်ဖြစ်သည်။ ထိုအချင်းအရာကို ရောင်ခြည်ဖြာစုတ်ယူခြင်း (radiation scattering and absorption) ဟုခေါ်သည်။ အလုံပိတ်အခန်းသည်အပူချိန်သုညတွင် အက်တမ်များတုန်ခါခြင်းမရှိတော့ပဲ ရောင်ခြည်များလည်းမရှိတော့သောကြောင့် ၎င်းကိုဝတ္ထုနက် (black body) ဟုခေါ်ဆိုသည်။

အလုံပိတ်အခန်းအတွင်းရှိ အက်တမ်များသည် တုန်ခါမှုကြောင့်ရောင်ခြည်ကိုထုတ်လွှတ်ပြီး ပြန်ကန်ထွက်လာသည့်ရောင်ခြည်များကိုလည်း စုတ်ယူခြင်းကြောင့် အချိန်တစ်ခုကြာသောအခါ မျှခြေအခြေအနေကို ရောက်ရှိမည်ဖြစ်သည်။ ထိုအခြေအနေတွင် အခန်းတွင်းရှိအပူချိန်နှင့် ရောင်ခြည်ပြင်းအားပမာဏများသည် ဆက်လက်ပြောင်းလဲခြင်းမရှိတော့ပဲ ကိန်းသေဖြစ်နေမည်။ ထိုအရာကို ရောင်ခြည်ဖြာထွက်ခြင်း−အပူမျှခြေ (thermal equilibrium of radiation) ဟုခေါ်ဆိုသည်။ ထိုအချိန်တွင်နံရံကိုအပေါက်သေးတစ်ခုဖောက်ပြီး အထဲမှရောင်ခြည်များကိုလေ့လာကြည့်ပါက ရောင်ခြည်များ၏ကြိမ်နှုန်း (frequency) နှင့်ပြင်းအားပမာဏကိုသိရှိနိုင်မည်။ ဆိုလိုသည်မှာ ကြိမ်နှုန်းနှင့်ပြင်းအားဆက်သွယ်ချက် (intensity spectrum) ကို သိရှိလိုခြင်းဖြစ်သည်။ Kinetic theory နှင့် စည်းချက်ကျတုန်ခါမှု (harmonic oscillation) သီအိုရီများကို ပေါင်းစပ်တွက်ထုတ်လိုက်ပါက အောက်ပါညီမျှခြင်းကိုရသည်။

I(\omega)=\frac{\omega^2kT}{\pi^2c^2}

$I(\omega)$ သည်ကြိမ်နှုန်းတစ်ခုအတွင်းရှိပြင်းအားကိုဖော်ပြပြီ: k နှင့် c သည် ကိန်းသေများဖြစ်ကာ T သည်အပူချိန်ဖြစ်သည်။ ယခုညီမျှခြင်းကို Rayleigh−Jeans law ဟုခေါ်သည်။ ဤညီမျှခြင်းအရ ပြင်းအားသည်ကြိမ်နှုန်းနှစ်ထပ်ကိန်းနှင့်တိုက်ရိုက်အချိုးကျကြောင်းကို တွေ့ရှိနိုင်သည်။ ထို့ကြောင့်ရောင်ခြည်၏ကြိမ်နှုန်းမြင့်လာပါက ပြင်းအားလည်းအလွန်မြင့်လာသည်၊ ကြိမ်နှုန်းမြင့်သော ခရမ်းလွန်ရောင်ခြည်နှင့် X-ray များသည်ပြင်းအားအလွန်ပင်များကြောင်း ခန့်မှန်းရသည်။ အောက်ပါပုံတွင် ကြိမ်နှုန်းနှင့်ပြင်းအားဂရပ်ကို ဆွဲပြထားသည်။ သီအိုရီခန့်မှန်းချက်မှာ မျဉ်းအပြည့်ဖြစ်သည်။

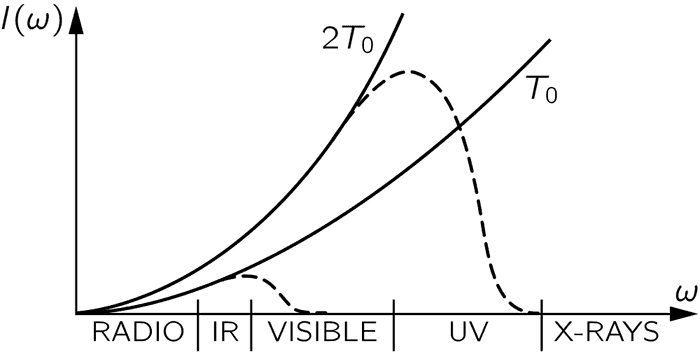
Black body ရောင်ခြည်ပြင်းအားဖြန့်ကျက်မှု

လက်ရှိညီမျှခြင်းအရ အခန်းအတွင်းမှအက်တမ်၊အီလက်ထရွန်များသည် အတန်အသင့်အပူချိန်နှင့် စွမ်းအင်ဖြင့်တုန်ခါနေကြသော်လည်း ထွက်လာသောရောင်ခြည်များမှာမူ အလွန်ပြင်းထန်လှသောကြောင့် ကြည့်ရှုနေသောသိပ္ပံပညာရှင်ပင်လျှင် မျက်စိကန်း၍ဓာတ်ရောင်ခြည်သင့်နိုင်လေသည်။ သို့သော်လက်တွေ့စမ်းသပ်ချက်များမှာမူ ဤကဲ့သို့မဟုတ်ပေ။ ကြိမ်နှုန်းအနိမ့်များတွင် ပြင်းအားပမာဏသည် သီအိုရီနှင့်ကိုက်ညီသော်လည်း ကြိမ်နှုန်းမြင့်လာပါက ပြင်းအားပမာဏကျဆင်းသွားပြီး X-ray များကိုလည်းထုတ်လွှတ်ခြင်းမတွေ့ရပေ။ အပေါ်ပုံထဲတွင် လက်တွေ့စမ်းသပ်ချက်ရလဒ်များကို အစက်မျဉ်းဖြင့်ပြထားသည်။ ဤပုံအရ ကြိမ်နှုန်းအမြင့်များအတွက် သီအိုရီခန့်မှန်းမှုမှားယွင်းကြောင်း ကောက်ချက်ချနိုင်သည်။ ထို့အပြင်အက်တမ်များ၏စုစုပေါင်းစွမ်းအင်သည် ဂရပ်အောက်ရှိဧရိယာဖြစ်သည့်အတွက် သီအိုရီမှခန့်မှန်းသောစွမ်းအင်သည် အလွန်များနေကြောင်းတွေ့ရှိနိုင်သည်။

Black body ရောင်ခြည်ထုတ်လွှင့်ခြင်းပြဿနာကို ၁၉ ရာစုသိပ္ပံပညာရှင်များသည် နည်းလမ်းအမျိုးမျိုးဖြင့်ဖြေရှင်းရန် ကြိုးစားကြသည်။ လက်ရှိသီအိုရီသည် ခရမ်းလွန်ရောင်ခြည်ပြင်းအားကို များစွာပို၍ခန့်မှန်းနေခြင်းကြောင့် ခရမ်းလွန်ကပ်ဘေးကျခြင်း ultraviolet catastrophe ဟုလည်းခေါ်ကြသည်။ ကြိမ်နှုန်း−ပြင်းအားဆက်သွယ်ချက်ကို ရှုထောင့်အမျိုးမျိုးမှချည်းကပ်သော်လည်း အဖြေမှာအတူတူပင်ဖြစ်နေသည့်အတွက် အရွေ့၊ အပူ၊ တုန်ခါမှု၊ ဓာတ်ရောင်ခြည်ရူပဗေဒသီအိုရီတစ်ခုခုသည် ချို့ယွင်းချက်ရှိနေကြောင်းမှန်းဆကြသည်။

၁၈၉၆ ခုနှစ်တွင် ဂျာမန်သိပ္ပံပညာရှင် Wilhelm Wien သည်လက်တွေ့စမ်းသပ်ချက်များမှရရှိသော ကြိမ်နှုန်း−ပြင်းအား အချက်အလက်များကိုအသုံးပြုပြီး လက်တွေ့ညီမျှခြင်း (empirical formula) တစ်ခုကိုထုတ်ဖော်ခဲ့သည်။ ထိုညီမျှခြင်းအရ ကြိမ်နှုန်းမြင့်လာပါက ရောင်ခြည်ပြင်းအားသည် ဆတိုးလျော့ကျ (exponential decay) သွားသည်။ ညီမျှခြင်းမှကိန်းသေများကို စမ်းသပ်ချက်များမှ ရယူရမည်ဖြစ်သည်။

u=\frac{\alpha \omega^3}{e^{\frac{\beta \omega}{T}}}

၁၈၉၉ ခုနှစ်တွင် ဂျာမန်သိပ္ပံပညာရှင် Max Planck သည် Wein ၏လက်တွေ့ညီမျှခြင်းကို သီအိုရီဖြင့်ဖော်ထုတ်ရန်ကြိုးပမ်းခဲ့သည်။ သူသည် Boltzmann ၏ kinetic theory of gases ကိုအခြေခံပြီး တုန်ခါမှုန်များ၏ အစဉ်မကျမှု (entropy) နှင့် စွမ်းအင်အကြောင်းကို မက်ကင်းနစ်နှင့်လျှပ်စစ်သံလိုက်ဥပဒေသများကို မမီခိုပဲဖော်ပြခဲ့သည်။ သို့သော် Planck သည် Boltzmann ၏ အက်တမ်ယူဆချက်နှင့် ဖြစ်တန်စွမ်းမက်ကင်းနစ် (statistical mechanics) ကိုအခြေခံသော သာမိုဒိုင်းနမစ်သီအိုရီကို လက်ခံခဲ့သူတစ်ဦးမဟုတ်ပေ။ Continuous matter အုပ်စုတွင်ပါဝင်သူဖြစ်သည်။ သူ၏တုန်ခါမှုန်သီအိုရီကိုလည်း အက်တမ်များတည်ရှိမှုကို မီခိုစေခြင်းမရှိအောင်ရေးသားခဲ့သည်။ ထိုသီအိုရီ၏ရလဒ်သည် Wein ၏ညီမျှခြင်းနှင့် ကိုက်ညီမှုရှိပြီး သီအိုရီပိုင်းတွင်လည်းစနစ်တကျရှိခဲ့သည်။ သို့သော်လည်း ထပ်မံရရှိသောစမ်းသပ်ချက်များအရ Planck-Wein ညီမျှခြင်းသည် ကြိမ်နှုန်းအနိမ့်များတွင် ကိုက်ညီမှုနည်းပါးကြောင်းတွေ့ရှိရပြန်သည်။

Planck သည် black body radiation အတွက် သူ၏သီအိုရီကို ပိုမိုကောင်းမွန်အောင်ပြုပြင်ရတော့မည်ဖြစ်သည်။ လက်တွေ့စမ်းသပ်ချက်များနှင့် ကိုက်ညီစေရန် နည်းမျိုးစုံကြိုးပမ်းသည်။ သူ၏ ၁၉၀၁ ခုနှစ်စာတမ်းတွင် တုန်ခါမှုန်များ၏ entropy နှင့်သူတို့၏ဖြစ်တန်စွမ်းကိုဖော်ပြရန် Boltzmann ၏ညီမျှခြင်းကို အသုံးပြုခဲ့သည်။ ထို့အပြင် တုန်ခါမှုန်များ၏စွမ်းအင်ကို အစဉ်အပြတ် (continuous) မဟုတ်စေပဲ အဆင့်လိုက်၊အဆင့်လိုက် (discrete) တန်ဖိုးများဖြင့်ယူဆရန်လိုအပ်သည်ဟုလည်း ဖော်ပြခဲ့သည်။ ထိုစာတမ်းအရ တုန်ခါမှုန်များ၏စွမ်းအင်သည် တောက်လျှောက်မဖြစ်နိုင်ပဲ အခြေခံစွမ်းအင်တစ်ခု၏ ဆပွားကိန်းများ (နှစ်ဆ၊ သုံးဆ၊ စသည်) သာဖြစ်နိုင်သည်ဟုဆိုသည်။ ညီမျှခြင်းဖြင့်ဖော်ပြလျှင်−

E=nh\omega

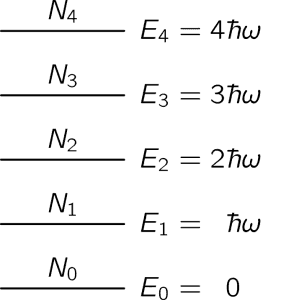
ဤနေရာတွင် n သည် ကိန်းပြည့်ဖြစ်ပြီး h သည် Planck ကိန်းသေဖြစ်သည်။ ထိုယူဆချက်ကိုသာ အခြေခံပါက တုန်ခါမှုန်များအားလုံး၏ပျမ်းမျှစွမ်းအင်သည်−

\overline{E}=\frac{h\omega}{e^{\frac{h\omega}{kT}-1}}

ဖြစ်၍ နောက်ဆုံးကြိမ်နှုန်း−ပြင်းအားညီမျှခြင်းသည်−

I(\omega)=\frac{h\omega^3}{\pi^2c^2(e^\frac{h\omega}{kT}-1)}

ဖြစ်သည်။ ဤညီမျှခြင်းအရ $\omega$ သုံးထပ်သည် ပိုင်းဝေတွင်ရှိသော်လည်း ပိုင်းခြေတွင် exponential ကိန်းကိုထပ်ညွှန်းများစွာတင်ထားသောကြောင့် ပြင်းအားဂရပ်သည် ထောင်တက်သွားခြင်းမရှိတော့ပေ။ ဤညီမျှခြင်းသည် စမ်းသပ်ချက်နှင့်လုံးဝကိုက်ညီခဲ့လေသည်။

Max Planck By Unknown - [1], Public Domain

သူ၏ "On the Law of Distribution of Energy in the Normal Spectrum" စာတမ်းပါသီအိုရီသည် အောင်မြင်မှုရရှိခဲ့သော်လည်း Planck သည် တုန်ခါမှုန်များ၏စွမ်းအင်ပမာဏအဆင့်ယူဆချက် (quantization) ကိုမူ စမ်းသပ်ချက်နှင့်ကိုက်ညီရန် လုပ်ဆောင်ရသောသင်္ချာဆိုင်ရာယူဆချက်တစ်ခုအနေဖြင့်သာ မှတ်ယူခဲ့ပြီး လက်တွေ့လောကတွင်အရေးပါခြင်းရှိ၊မရှိကို သူ၏စာတမ်းတွင် မဖော်ပြခဲ့ပေ။ ၁၉၀၆ ခုနှစ်အထိ ငါးနှစ်အတွင်းတွင်လည်း ဤအကြောင်းကိုထပ်မံဖော်ထုတ်ခဲ့ခြင်းမရှိပေ။ အခြေခံကျသောရူပဗေဒသီအိုရီများကိုနှစ်သက်သော Planck သည်သူ၏သီအိုရီသည် မူလရူပဗေဒ (classical physics) မှကွဲထွက်နေသည်ဟု မမှတ်ယူခဲ့ပေ။ သိပ္ပံပညာရှင် Lorentz အစရှိသောပုဂ္ဂိုလ်များ၏ ဖော်ထုတ်ချက်များကြောင့်သာ ၁၉၀၈ ခုနှစ်တွင် သူ့သီအိုရီကို လက်ရှိရူပဗေဒဥပဒေသများဖြင့် မတွက်ထုတ်နိုင်ကြောင်းဝန်ခံခဲ့သည်။ နောင်လာမည့်နှစ်များတွင်မူ Planck က quantized စွမ်းအင်သီအိုရီသည် ရူပဗေဒ၏လက်တွေ့ကျသော အခြေခံအုတ်မြစ်တစ်ခုဖြစ်ကြောင်း အခြားသိပ္ပံပညာရှင်များနှင့်အတူ ဂုဏ်ယူစွာလက်ခံခဲ့လေသည်။

Planck ၏သီအိုရီထွက်ရှိလာသော ၂၀ ရာစုနှစ်အစပိုင်းတွင် သိပ္ပံပညာရှင် Albert Einstein ဆိုသူသည် ထိုသီအိုရီနှင့် Maxwell ညီမျှခြင်းများကိုအခြေခံ၍ ၁၉၀၅ ခုနှစ်တွင် အလင်းမှုန် photon သည် စွမ်းအင်အဆင့် (quanta) ကိုလိုက်နာသောအမှုန်တစ်မျိုးဖြစ်ကြောင်း ဖော်ထုတ်ခဲ့သည်။ ထို့ပြင် ၁၉၀၇ ခုနှစ်တွင် ဒြပ်ထုများ၏ အပူသိုလှောင်မှု (specific heat) အကြောင်းကို quantum သီအိုရီအသုံးပြု၍ တွက်ထုတ်ခဲ့သည်။ ဤအခြင်းအရာများအရ Einstein သည် Planck ထက်စော၍ ကွမ်တမ်ဥပဒေသကိုလက်ခံခဲ့သည်ဟု မှတ်ချက်ပြုကြသည်။ မည်သို့ပင်ဆိုစေကာမူ Planck နှင့် Einstein နှစ်ယောက်စလုံး သူတို့၏တွေ့ရှိချက်များအတွက် နိုဘယ်ဆုအသီးသီးရရှိခဲ့ကြပြီး ကွမ်တမ်သီအိုရီသည် သိပ္ပံပညာရှင်များကို နောင်ရာစုနှစ်တိုင်အောင်ဂယက်ရိုက်စေခဲ့သော ခေတ်သစ်သိပ္ပံကို မွေးဖွားခဲ့လေသည်။

၁၉၁၁ Solvay ကွန်ဖရင့်ပလန့်−မတ်တပ်ရပ်ဘယ်ဘက်မှဒုတိယ၊ အိုင်းစတိုင်း−မတ်တပ်ရပ်ညာဘက်မှဒုတိယBy Benjamin Couprie - Benjamin Couprie, Public Domain

References:
http://www.feynmanlectures.caltech.edu/I_41.html
https://readingfeynman.org/tag/uv-catastrophe/
https://pdfs.semanticscholar.org/7aeb/37159b682b0e5ce54cdeb2834ccb4dbcd5be.pdf
http://strangepaths.com/files/planck1901.pdf
Timeline of thermodynamics - Wikipedia

It is not the possession of truth, but the success which attends the seeking after it, that enriches the seeker and brings happiness to him.

Max Planck