လည်ခြင်းစနစ်များ (Rotations) - Part 3

5 December 2017

ထောင့်ပြောင်းအဟုန် (Angular momentum)

၅ ပေလောက်အရှည်ရှိတဲ့ ဝါးလုံးတစ်လုံးကို တူညီတဲ့နှုန်းနဲ့ အလယ်က ကိုင်လှည့်တာနဲ့ အဖျားကလှည့်တာ ဘယ်ဟာပိုခက်မယ်ထင်ပါသလဲ။ နောက်တစ်ခါ ပြင်ပအားသက်ရောက်မှုမရှိပဲနဲ့ လည်ပတ်နှုန်းကိုပြောင်းလို့ရော ရနိုင်ပါသလား။ ဒီအပိုင်းကို ဖတ်ပြီးသွားရင် ဒီမေးခွန်းတွေရဲ့အဖြေကို နားလည်နိုင်မှာဖြစ်ပါတယ်။

နယူတန်ဒုတိယနိယာမအရ အားက အဟုန်ပြောင်းလဲနှုန်းနဲ့ တိုက်ရိုက်အချိုးကျပါတယ်။ အားသက်ရောက်မှုတစ်ခုရှိရင် အဟုန်တိုးလာပါမယ်။

\vec{F}=\cfrac{d\vec{p}}{dt}

ဒီတော့ အားနဲ့ လိမ်အားတို့ နှိုင်းယှဉ်ချက်အရ လိမ်အားက ထောင့်ပြောင်းအဟုန်ပြောင်းလဲမှုကို ဖြစ်ပေါ်စေတယ်လို့ ခန့်မှန်းနိုင်ပါတယ်။ ပွတ်မှုအားနဲ့ စွမ်းအင်ဆုံးရှုံးမှုတွေမရှိရင်၊ ပြင်ပလိမ်အားသက်ရောက်မှုလည်းမရှိရင် လည်နေတဲ့အရာတစ်ခုက ဆက်လည်နေမယ်လို့ ခန့်မှန်းနိုင်ပါတယ်။ $\vec{F}$ နဲ့ $\vec{r}$ ကိုမြှောက်ရင် လိမ်အား $\vec{\tau}$ ကိုရပြီး $\tau$ ရဲ့ ဦးတည်ရာက rotation plane ကို ထောင့်မှန်ကျတယ်ဆိုတာ သိပြီ:ပါပြီ။ အခုဆက်ပြောမယ့်အပိုင်းတွေမှာ $\tau$ ရဲ့ component သုံးကြောင်းစီ မရေးချင်တဲ့အတွက် principal plane rotation ကိုသုံးပြီး $\tau$ component တစ်ခုပဲရှိတယ် လို့ ယူဆကြစို့။

\tau = F.r

နယူတန်ဒုတိယနိယာမအရ−

F=\cfrac{dp}{dt}=m\cfrac{dv}{dt}

But $v=r.\omega$

အခု လောလောဆယ် ဝတ္ထုကိုဖွဲ့ စည်းထားတဲ့ အမှုန်အများကြီးထဲက အမှုန်တစ်မှုန်စာကိုပဲ စဉ်းစားပါမယ်။ $F$ က အမှုန်ပေါ်မှာ သက်ရောက်တယ်ဆိုရင် $F\cdot r$ က $r$ နဲ့ $v=r\cdot \omega$ က $r$ တို့က အတူတူပဲဖြစ်ပါမယ်။

F= m\cfrac{dv}{dt} = m.r\cfrac{d\omega }{dt}

$\frac{d\omega }{dt}$ က သင်ထင်တဲ့အတိုင်း ထောင့်ပြောင်းအရှိန်ကိုပြောဖြစ်ပြီ: $\dot{\omega }$ လို့လည်းရေးပါတယ်။ ဒီတော့−

\tau=F.r=mr^2\cfrac{d\omega }{dt}

ဒီညီမျှခြင်းကို $F=m\frac{dv}{dt}$ နဲ့ နှိုင်းယှဉ်ကြည့်ရင် $\tau$ က $F$ နဲ့ဆင်တူပြီး၊ $\omega$ က $v$ နဲ့ဆင်တူတယ်ဆိုရင် $mr^2$ က $m$ နဲ့ ဆင်တူတာကို တွေ့ရပါမယ်။ ဒြပ်ထုလိုမျိုး အင်နားရှားသဘောကိုဆောင်တာကြောင့် $mr^2$ ကိန်းကို moment of inertia လို့ခေါ်ပါတယ်။ moment ဆိုတာက lever သဘောကို ပြတဲ့စကားလုံးတစ်ခုပဲဖြစ်ပါတယ်။ Moment of inertia ကို သင်္ကေတ $I$ နဲ့ ပြလေ့ရှိပါတယ်။ ဝတ္ထုတစ်ခုကို အမှုန်သေးသေးလေးတွေ အများကြီးနဲ့ ဖွဲ့စည်းထားတဲ့အတွက် ဝတ္ထုရဲ့ $I$ စုစုပေါင်းကိုလိုချင်ရင် အမှုန်လေးတွေရဲ့ $I$ အားလုံးပေါင်းပေးရပါမယ်။

I=\sum m_i r_i^2

ဥပမာတစ်ခုအနေနဲ့ ဝါးလုံးလိုမျိုး ဆလင်ဒါပုံစံအချောင်းတစ်ချောင်းရဲ့ moment of inertia ကို ရှာကြည့်ပါမယ်။ အရင်ဆုံး ဝါးလုံးအဖျားကနေ လှည့်ကြည့်ပါမယ်။

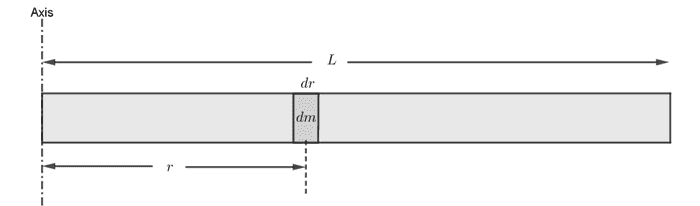
ဝါးလုံးရဲ့ ကန့်လန့်ဖြတ်ပိုင်းပုံက စက်ဝိုင်းပုံရှိတဲ့အတွက် ဝါးလုံးကိုစက်ဝိုင်းပြားလေးတွေအများကြီးနဲ့ ဖွဲ့စည်းထားတယ်လို့ မြင်ကြည့်ပါ။ ဒါဆို စက်ဝိုင်းပြားတစ်ခုစီမှာ ဒြပ်ထု $m_i$ နဲ့ ဝင်ရိုးကအကွာအဝး $r_i$ တို့ရှိပါမယ်။

I=\sum m_i r_i^2 = \int r^2 dm

ဝါးလုံးရဲ့ ကန့်လန့်ဖြတ်ဧရိယာက A ဖြစ်ပြီး သိပ်သည်းဆက $\rho$ ဖြစ်မယ်ဆိုရင်−

dm=\rho A.dr

\text{So, } I=\rho A \int r^2 dr=\rho A \cfrac{L^3}{3}=m \cfrac{L^2}{3}

နောက်တစ်ခါ ဝါးလုံးရဲ့ဒြပ်ထုဗဟိုချက်ဖြစ်တဲ့ အလယ်တည့်တည့်ကိုဝင်ရိုးထားပြီး လှည့်ကြည့်ပါမယ်။

ဒီအခြေအနေကို အလျား $\frac{L}{2}$ ရှိတဲ့ ဝါးလုံးနှစ်လုံးကို အစွန်ကလှည့်တယ်လို့လည်း မြင်နိုင်ပါတယ်။ ဒီေတာ့−

I=2 \cfrac{m}{2} \cfrac{(\cfrac{L}{2})^2}{3}=m \cfrac{L^2}{12}

ဒါကြောင့် ဝါးလုံးကို အလယ်ကနေလှည့်ရင် moment of inertia နည်းတဲ့အတွက် အဖျားကလှည့်တာထက် ပိုပြီးလွယ်ကူပါတယ်။

လည်ပတ်တဲ့ ဝင်ရိုးက ဝတ္ထုရဲ့ဒြပ်ထုဗဟိုချက်မှာ မဟုတ်တဲ့ (ဥပမာ ဝါးလုံးကို အဖျားကလှည့်တာမျိုး) စနစ်ေတွအတွက် မူလညီမျှခြင်း $\int r^2 dm$ နဲ့တွက်လို့ရသလို ပိုမြန်တဲ့နည်းလမ်းတစ်ခုနဲ့လည်း တွက်လို့ရပါတယ်။ ဒါကေတာ့ ဝတ္ထုရဲ့ဒြပ်ထုစုစုပေါင်းကို ဒြပ်ထုဗဟိုချက်မှာ စုစည်းစေလိုက်ပြီး အဲ့လောက်ဒြပ်ထုရှိတဲ့ အမှုန်တစ်ခုအနေနဲ့ပဲ ရွေ့လျားစေတာဖြစ်ပါတယ်။ ဒါဆိုရင် အဲ့ဒီ့အမှုန်ရဲ့ $I$ ကို $mr^2$ နဲ့တွက်လို့ရပါမယ်။ ဒါပေမယ့်ဒါက ဒြပ်ထုဗဟိုချက်ရွေ့တာကိုပဲ စဉ်းစားထားတာဖြစ်ပါတယ်။ အရွယ်အစားရှိတဲ့ပစ္စည်း (ဥပမာ သံလုံးတစ်လုံး)ကို လှည့်တဲ့အခါ $mr^2$ နဲ့တွက်ရင် မှားပါလိမ့်မယ်။ ဘာကြောင့်လဲဆိုတော့ ဝတ္ထုက ပြင်ပဝင်ရိုးကိုပတ်လည်ရုံသာမက သူ့ရဲ့ဒြပ်ထုဗဟိုချက်မှာပါ လည်နေတာကြောင့်ဖြစ်ပါတယ်။ ဒါကိုပိုပြီ:သိသာစေဖို့အတွက် ဒြပ်ထုဗဆိုချက်မှာ reference frame နောက်တစ်ခု (x’, y’) ကိုထားကြည့်ပါမယ်။ ဒါဆိုရင် frame (x’, y’) ကိုယ်တိုင်က ဝင်ရိုးကိုပတ်ပြီးလည်နေပါမယ်။ ဒီ frame ကနေပြီး သံလုံးပေါ်မှာရှိတဲ့ အမှုန်လေးတစ်ခုရဲ့ရွေ့လျားမှုကို စစ်ဆေးကြည့်ပါမယ်။ အောက်ကပုံမှာ အနီစက်လေးက သံလုံးမျက်နှာပြင်ပေါ်မှာရှိတဲ့ အမှုန်တစ်ခုဖြစ်ပါတယ်။ သံလုံးနဲ့ ဝင်ရိုးကိုဆက်သွယ်ထားတဲ့ အချောင်းရဲ့ ဒြပ်ထုကိုတော့ လျစ်လျူရှုနိုင်ပါတယ်။

အပေါ်ကပုံအရ သံလုံးကိုဖွဲ့စည်းထားတဲ့အမှုန်တွေက frame (x, y) ကို ပတ်ပြီး လည်နေရုံသာမကပဲ သံလုံးရဲ့ ဒြပ်ထုဗဟိုချက်ကိုပါ ပတ်ပြီးလည်နေတာကို တွေ့ရပါတယ်။ ဝတ္ထုရဲ့အပြင်မှာရှိတဲ့ ဝင်ရိုးကို ပတ်ပြီးလည်တာကို revolve လို့ခေါ်ပြီး ဒြပ်ထုဗဟိုချက်ကိုပတ်ပြီးလည်တာကို rotate လို့ခေါ်ပါတယ်။ ဒါဆို ကိုယ်ပိုင်ဗဟိုချက်ကို ပတ်လည်ဖို့လိုတဲ့ moment of inertia ကိုပါ ထပ်ရှာရပါမယ်။

ဝတ္ထု (ဥပမာ သံလုံး) ကို အမှုန်သေးသေးလေးေတွအများကြီးနဲ့ ဖွဲ့စည်းထားပါတယ်။ ဒီအမှုန်တစ်မှုန်ချင်းစီမှာ ဒြပ်ထု $m_i$ နဲ့ ဒြပ်ထုဗဟိုချက်က အကွာအဝေး $r_i$ ရှိတဲ့အတွက် moment of inertia လည်း ကိုယ်စီရှိပါတယ်။ အမှုန်တွေအကုန်လုံးက moment of inertia ေတွအားလုံးပေါင်းလိုက်ရင် ဝတ္ထုရဲ့ ဒြပ်ထုဗဟိုချက်မှာရှိတဲ့ moment of inertia ကို ရပါမယ်။

I_{CM}=\sum m_i r_i^2=\int r^2 dm

ဒါဆိုရင် စောစောက သံလုံးပတ်လည်တဲ့ပုံအတွက်−

I = \underbrace{I_{CM}}_{\text{due to rotation}} + \underbrace{MR^2}_\text{due to revolving}

ဒီညီမျှခြင်းကို parallel axis theorem လို့ခေါ်ပါတယ်။ ဒြပ်ထုဗဟိုချက်ကိုဖြတ်သွားတဲ့ ဝင်ရိုးနဲ့ ပတ်နေတဲ့ဝင်ရိုးကြားက အကွာအဝေးက $R$ ဖြစ်ပြီး ဝင်ရိုးနှစ်ခုက အပြိုင်ဖြစ်ရပါမယ်။ ပုံမှန်ပုံသဏ္ဍာန် (လေးထောင့်၊ အဝိုင်း၊ ဆလင်ဒါ) ရှိတဲ့ ပစ္စည်းတွေရဲ့ ဒြပ်ထုဗဟိုချက်မှာရှိတဲ့ moment of inertia ေတွကို ပြုစုထားတဲ့ ဇယားေတွရှိတဲ့အတွက် အပြင် ဝင်ရိုးမှာရှိတဲ့ moment of inertia ကို လိုချင်ရင် parallel axis formula နဲ့ တွက်လိုက်ရုံပါပဲ။

အားနဲ့ လိမ်အားတို့ရဲ့ ဆက်စပ်ချက်အရ လိမ်အားက ထောင့်ပြောင်းအဟုန်ပြောင်းလဲမှုကို ဖြစ်ပေါ်စေပါတယ်။ ထောင့်ပြောင်းအဟုန် ညီမျှခြင်းကို ရှာဖို့အတွက် လိမ်အားညီမျှခြင်းကို ပြန်ကြည့်ပါမယ်။

\tau=mr^2 \cfrac{d\omega }{dt}= \cfrac{d(I \omega )}{dt} = \cfrac{dL}{dt}

အပေါ်က ရလဒ်အရ ထောင့်ပြောင်းအဟုန်ညီမျှခြင်းက−

L=I.\omega

Vector ပုံစံနဲ့ရေးရင်−

\vec{L}=I \vec{\omega }

$\vec{L}$ ရဲ့ ဦးတည်ရာက $\vec{\tau }$ လိုပဲ rotational plane ကို ထောင့်မှန်ကျပြီး ညာလက်ထုံးကို လိုက်နာပါတယ်။ $L$ ကို မျည်းဖြောင့်အဟုန် (linear momentum) နဲ့လည်း ဆက်နွယ်ပြီး ရှာလို့ရပါသေးတယ်။ အားတစ်ခုက မျည်းဖြောင့်အဟုန်ပြောင်းလဲနှုန်းကို ဖြစ်ပေါ်စေပါတယ်။ တကယ်လို့ ဝင်ရိုးကိုပတ်လည်နေတဲ့အရာဆိုရင် အမှုန်တစ်ခုအတွက်−

\tau = F.r=\cfrac{dp}{dt} .r=\cfrac{dp.r}{dt}

ထုံးစံအတိုင်း $p$ နဲ့ $r$ က ထောင့်မှန်ကျရမှာဖြစ်ပြီး ထောင့်မှန်မကျရင် component ခွဲတွက်ရမှာဖြစ်ပါတယ်။ Vector ပုံစံနဲ့ဆိုရင်−

\vec{L}=\vec{p} \times \vec{r}

ဝတ္ထုတစ်ခုလုံးအတွက်ဆိုရင် $L$ တွေအားလုံးပေါင်းရမှာ ဖြစ်ပါတယ်။

ထောင့်ပြောင်းအဟုန်တည်မြဲခြင်းနိယာမ (Angular momentum)

နယူတန် တတိယနိယာမအရ စနစ်တစ်ခုအတွင်းမှာ သက်ရောက်အားနဲ့ တန်ပြန်သက်ရောက်အားေတွက တူညီတဲ့အတွက် ပြင်ပသက်ရောက်အားကသာ အဟုန်ပြောင်းလဲမှုကို ဖြစ်ပေါ်စေနိုင်ပါတယ်။ လိမ်အားကလည်း အားနဲ့ အကွာအဝေးနဲ့ မြှောက်ရတဲ့အတွက် ပြင်ပလိမ်အားကသာ ထောင့်ပြောင်းအဟုန်ပြောင်းလဲမှုကို ဖြစ်ပေါ်စေနိုင်ပါတယ်။ ဒီတော့ ပြင်ပလိမ်အားသက်ရောက်မှုမရှိရင် ထောင့်ပြောင်းအဟုန်က စနစ်အတွင်းမှာ ကိန်းသေဖြစ်ပါတယ်။

\vec{L}=I \vec{\omega }=\vec{p} \times \vec{r}

Linear momentum မှာ mass $(m)$ က ကိန်းသေဖြစ်ပေမယ့် angular momentum မှာ moment of inertia $(I)$ က ဝင်ရိုးက အကွာအဝေး $(r^2)$ ကို မူတည်ပါတယ်။ ဒီတော့ $L$ က ကိန်းသေဖြစ်ပေမယ့် $I$ ကို လျှော့ချလိုက်ရင် $\omega$ က တိုးလာမှာဖြစ်ပြီး $I$ ကို တိုးလိုက်ရင် $\omega$ က လျော့သွားမှာဖြစ်ပါတယ်။ ဒီဥပဒေသကို အောက်က video မှာ လက်တွေ့စမ်းပြထားတာ တွေ့နိုင်ပါတယ်။

အလေးတုံးတွေကို ဆန့်ထုတ်လိုက်တဲ့အချိန်မှာ radius တိုးသွားတဲ့အတွက် $I$ များလာပြီး လည်နှုန်းလျော့သွားတာကို မြင်နိုင်ပါတယ်။ ဝင်ရိုးနဲ့ ကပ်လိုက်ရင်တော့ moment of inertia နည်းသွားပြီး လည်နှုန်းပိုမြန်လာတာကို မြင်နိုင်ပါတယ်။ ဒါကြောင့် ပြင်ပလိမ်အားသက်ရောက်မှုမရှိပဲ ကိုယ့်ရဲ့ လည်ပတ်နှုန်းကို ပြောင်းလဲနိုင်ပါတယ်။