Ordinary Differential Equations - Part 3

19 July 2018

Free damped oscillation အတွက် အချိန်အလိုက်ပြောင်းလဲတဲ့ $x$ ရဲ့အဖြေကိုရှေ့အပိုင်းမှာတွက်ထုတ်ခဲ့ပါတယ်။

x=Ae^{(-\gamma \pm \sqrt{\gamma^2 - \omega_0 ^2})t}

Constant A က x-t graph ရဲ့ စကေးကိုပဲပြောင်းလဲစေတာဖြစ်တဲ့အတွက် လောလောဆယ်ကျွန်တော်တို့ initial condition တွေက သူ့ကို 1 ဖြစ်စေတယ်ဆိုပါတော့။

x=e^{(-\gamma \pm \sqrt{\gamma^2 - \omega_0 ^2})t}

$\omega_0$ နဲ့ $\gamma$ နဲ့နှိုင်းယှဉ်လိုက်ရင် အခြေအနေသုံးခုဖြစ်နိုင်ပါတယ်။

\omega_0 > \gamma \ \text{(underdamped)}

\omega_0 = \gamma \ \text{(critically damped)}

\omega_0 < \gamma \ \text{(overdamped)}

ပထမအခြေအနေဖြစ်တဲ့ $\omega_0 > \gamma$ ဆိုရင် square root ထဲကကိန်းက အနှုတ်ကိန်းဖြစ်ပါမယ်။ ဒီတော့ exponential ပေါ်မှာ imaginary ကိန်းအနေနဲ့ရေးပါမယ်။

x= e^{(-\gamma \pm i  \sqrt{\omega_0 ^2 - \gamma^2})t}

x=e^{-\gamma t}e^{\pm i t \sqrt{\omega_0 ^2 - \gamma^2}}

x=e^{-\gamma t}[Ae^{ i t \sqrt{\omega_0 ^2 - \gamma^2}}+Be^{- i t \sqrt{\omega_0 ^2 - \gamma^2}}]

နောက်ဆုံးညီမျှခြင်းက သူ့အပေါ်က solution နှစ်ခုပေါင်းပြီးရေးထားတာပဲဖြစ်ပါတယ်။

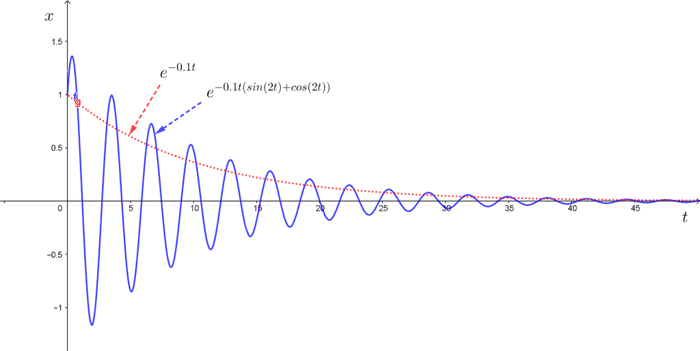
အပေါ်ကအဖြေကိုလေ့လာကြည့်ရင် real negative exponential တစ်ခုနဲ့ imaginary exponential function တို့ကိုတွဲထားတာတွေ့နိုင်ပါတယ်။ Imaginary exponential function ရဲ့သဘာဝက oscillating ဖြစ်နေမှာဖြစ်ပြီး real negative exponential ကတော့ အချိန်အလိုက် exponentially ထိုးကျသွားမှာဖြစ်တယ်။ ဒီတော့ underdamped case မှာ $\gamma t >> 1$ ဖြစ်လာတာနဲ့ $x$ ကအလွန်နည်းသွားမှာဖြစ်ပါတယ်။

ဒုတိယတစ်ခုဖြစ်တဲ့ critically damp case မှာတော့ $x=e^{-\gamma t}$ (general solution ဆိုရင် $x=(A+Bt)e^{-\gamma t}$ ) သာရတာကြောင့် oscillation လုံးဝမဖြစ်ပါဘူး။

တတိယတစ်ခု overdamped case မှာဆိုရင် falling exponential နှစ်ခုရှိပါမယ်။ ပေါင်းရေးလိုက်ရင်−

x= e^{-\gamma t}[Ae^{t \sqrt{\gamma^2 - \omega_0 ^2}}+Be^{-t \sqrt{\gamma^2 - \omega_0 ^2}}]

ရပါမယ်။

ဟုတ်ပြီ။ အခု forced oscillation ကိုကြည့်ရအောင်။ အရင်ကအတိုင်းပဲ force က amplitude $f_0$ နဲ့ frequency $\omega$ နဲ့ oscillation ဖြစ်နေတယ်လို့ယူဆပါမယ်။ ဒါဆိုရင် force equation (equation of motion) က−

m \frac{d^2x}{dt^2}+c \frac{dx}{dt}+kx=f(t)=f_0e^{i\omega t}

ဒီ equation က linear ဖြစ်ပြီး applied force က imaginary component မရှိတဲ့အတွက် အဖြေမှာ real part ကိုပဲယူရပါမယ်။ ဒါပေမယ့် $x^0$ ဖြစ်တဲ့ force term ပါနေတဲ့အတွက် homogeneous တော့မဟုတ်ပါဘူး။ အခု အဲ့ဒီ့ equation အတွက်အဖြေတစ်ခုကိုခန့်မှန်းကြည့်ပါမယ်။

_Ansatz

x=Ae^{i\omega t}

_(Ansatz = ခန့်မှန်းအဖြေ)

Displatement $x$ က forced frequency $\omega$ အတိုင်း oscillate ဖြစ်နေမယ်လို့ ခန့်မှန်းပါမယ်။ မူလ equation of motion မှာအစားသွင်းပြီး x ကိုဖြေရှင်းလိုက်ရင်−

x(t)=\frac{f_0e^{i\omega t}}{-m A  \omega ^2 e^{i\omega t}+c A i \omega e^{i\omega t} + k A e^{i\omega t} }

x(t)=\frac{f_0}{-m A  \omega ^2+c A i \omega + k A}

ဒီ $x(t)$ ( $x_{\text{forced}}(t)$ လို့ခေါ်လိုက်ပါမယ်) ကအဖြေတစ်ခုဖြစ်ပေမယ့် ပြည့်စုံတဲ့အဖြေတော့မဟုတ်သေးပါဘူး။ ဘာလို့လဲဆိုတော့ forced oscillation ညီမျှခြင်းမှာ force term ကို 0 ပေးပြီးတွက်လိုက်ရင် free oscillation ကအဖြေကိုရပါမယ်။ ဆိုလိုတာက အပေါ်ဆုံးမှာဆွေးနွေးသွားတဲ့ free oscillation အတွက်အဖြေ $x_{\text{free}}(t)$ ကိုထည့်တွက်လိုက်ရင် 0 ရပါလိမ့်မယ်။ 0 ရတာ လိုချင်တဲ့ $f(t)$ ရတာမဟုတ်တဲ့အတွက် forced oscillation ရဲ့အဖြေမဟုတ်ဘူးလို့ ထင်ကောင်းထင်ပါလိမ့်မယ်။ ဒါပေမယ့် $f(t)=f(t)+0$ လို့ လုံးဝရေးလို့ရပါတယ်။ ဒီတော့ $x_{\text{free}}(t)$ ကသူ့ချည်းသက်သက်အဖြေမဖြစ်နိုင်ပေမယ့် linear ODE ရဲ့ superposition ဂုဏ်သတ္တိအရ $x_{\text{forced}}(t)+x_{\text{free}}(t)$ ကတော့ အဖြေတစ်ခုဖြစ်ပါတယ်။ ဒီတော့ forced oscillation အတွက်ယေဘူယျအကျဆုံး solution က−

x=\frac{f_0}{-m A \omega ^2+c A i \omega + k A}+ Be^{-\gamma t}[e^{t\sqrt{\gamma^2 - \omega_0 ^2}}+e^{-t\sqrt{\gamma^2 - \omega_0 ^2}}]

ပထမ term က သိတဲ့အတိုင်း force ကြောင့်ဖြစ်တဲ့ oscillation ဖြစ်ပြီး ဒုတိယ term က initial disturbance ပေးလိုက်ရင်ဖြစ်တဲ့ free oscillation ဖြစ်ပါတယ်။ ဒီတော့ forced oscillation ရဲ့ယေဘူယျအကျဆုံးအဖြေက force ကြောင့်ဖြစ်တဲ့ oscillation နဲ့ free oscillation ကိုပေါင်းစပ်ထားတာဖြစ်ပါတယ်။ ဒါပေမယ့် free oscillation term က အလျင်အမြန်ပဲပျောက်ကွယ်သွားပါတယ် (exponentially decay ဖြစ်တယ်လို့ခေါ်ပါတယ်)။ ဒါကြောင့် free oscillation term ကို သက်တမ်းတိုတုန့်ပြန်မှု (transient response) လို့ခေါ်ပါတယ်။ အချိန်ကြာလာရင် forced oscillation term သာကျန်နေတာမို့သူ့ကို ပုံမှန်တုန့်ပြန်မှု (steady state response) လို့ခေါ်ပါတယ်။

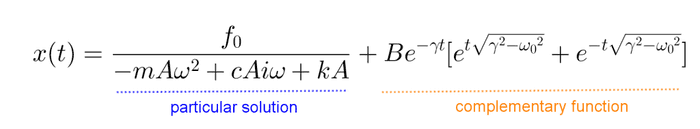
သင်္ချာသဘောတရားအရပြောရရင် inhomogeneous ODE ရဲ့ ယေဘူကျအကျဆုံး solution မှာ ညာဘက်က $x^0$ term ကို 0 ပေးလိုက်လို့ရတဲ့ homogeneous ODE ရဲ့ solution ပါတွဲပါနေတာကို တွေ့နိုင်ပါတယ်။ သင်္ချာအခေါ်အဝေါ်အရ ပထမ solution ကို particular solution လို့ခေါ်ပြီး ဒုတိယ solution ကို complementary function လို့ခေါ်ပါတယ်။

Better to light a candle than curse the darkness

~Peter Benenson