Gravity inside a Hollow Earth
28 August 2017
gravityHollow earth society က လူတွေပြောသလို ကမ္ဘာကြီးက အခေါင်းပေါက်ကြီးဆိုရင် ကမ္ဘာအတွင်းပိုင်းမှာနေတဲ့ လူတွေက အိမ်မြှောင်တွေလို ဇောက်ထိုးကပ်နေမှာမဟုတ်ပဲ ဟင်းလင်းပြင်ထဲမှာလို လွင့်မြောနေကြလိမ့်မယ်။ ဘာလို့လဲဆိုတော့ အခေါင်းပေါက်ကမ္ဘာအတွင်းမှာဆိုရင် ဘယ်နေရာမှာပဲဖြစ်ဖြစ် မြေဆွဲအားက သုညဖြစ်နေလို့ပဲ။
ဒီလိုဖြစ်ရတာဟာ မြေဆွဲအားက ဒြပ်ထုနှစ်ခုအကွာအဝေးနှစ်ထပ်ကိန်းနဲ့ ပြောင်းပြန်အချိုးကျလို့ပဲဖြစ�်တယ်။ ဒါပေမယ့် စက်လုံးရဲ့ မျက်နှာပြင်ဧရိယာ (ထို့ကြောင့် ဒြပ်ထု) က အချင်းဝက်နှစ်ထပ်ကိန်းနဲ့ တိုက်ရိုက်အချိုးကျတယ်။ စက်လုံးရဲ့ အလယ်ဗဟိုမှာဆိုရင်တော့ ဒြပ်ဆွဲအားတွေ မျှခြေဖြစ်သွားတာရှင်းပါတယ်။ ဒါပေမယ့် ဗဟိုမဟုတ်ရင်လည်း နှစ်ထပ်ကိန်းအချိုးက တူညီနေတဲ့အတွက် အားသက်ရောက်မှုရှိမှာမဟုတ်ပါဘူး။
စက်လုံးကို မစဉ်းစားသေးပဲ 2D ဖြစ်တဲ့ စက်ဝိုင်းကို စဉ်းစားကြည့်။ P က စက်ဝိုင်းအထဲက ကြိုက်တဲ့အမှတ်တစ်ခုမှာရှိမယ်။ လူက အမှတ် P မှာ ရှိတယ်။ ပြီ:ရင် လူကို ဗဟိုပြုပြီး ထောင့်အသေးလေး dθ တစ်ခု ဆန့်ထုတ်လိုက်။ သူ့ဆန့်ကျင်ဘက်ကိုလည်း ဆွဲထုတ်လိုက်။
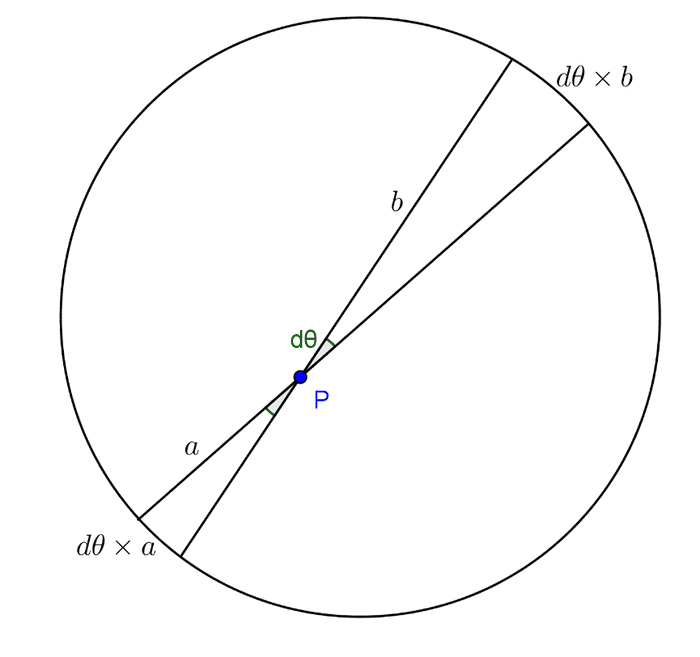
အဲ့ဒါဆိုရင် အဲ့ဒီ့ထောင့် dθ က အုပ်မိတဲ့ စက်ဝိုင်းရဲ့ မျက်နှာပြင်အရှည် (စက်ဝန်းပိုင်း) က တစ်ဖက်မှာ dθ × a ဖြစ်ပြီး နောက်တစ်ဖက်မှာ dθ × b ဖြစ်လိမ့်မယ်။ စက်လုံးမှာဆိုရင် ထောင့်က ကတော့ချွန်ပုံရှိပြီး အုပ်မိတာက စက်လုံးရဲ့ မျက်နှာပြင်ဧရိယာဖြစ်လိမ့်မယ်။
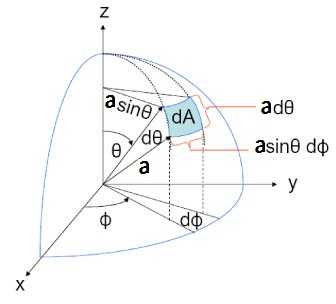
Image source: Stack Exchange
စက်လုံးရဲ့ အထူက ဖြစ်မယ်ဆိုရင် ထုထည်က−
က သိပ်သည်းဆဆိုရင် ဒြပ်ထုက−
အခု စက်လုံးအပိုင်းတစ်ခုစီက အမှတ် P မှာရှိတဲ့ လူပေါ်ကို သက်ရောက်တဲ့ ဒြပ်ဆွဲအားကို ရှာရအ�ောင်။ ဒြပ်ဆွဲအား ညီမျှခြင်းက ဆိုတော့ လူရဲ့ ဒြပ်ထုက ဖြစ်မယ်ဆိုရင် ဘယ်ဘက်ခြမ်းက အပိုင်းလေးက သက်ရောက်တဲ့အားက−
ဖြစ်မယ်။
အလားတူပဲ ညာဘက်ခြမ်းက အပိုင်းလေး သက်ရောက်တဲ့အားက−
ဖြစ်မယ်။
အဲ့ဒီ့တော့ ဘယ်ဘက်ခြမ်းက ဒြပ်ထုအပိုင်းလေးဆွဲတဲ့အားနဲ့ ညာဘက်ခြမ်းက အပိုင်းလေးဆွဲတဲ့အားက အတူတူပဲဆိုတာတွေ့ရမယ်။ စက်လုံးတစ်ခုလုံးကို အဲ့ဒီ့လို အပိုင်းလေးအတွဲတွေ အများကြီးနဲ့ ဖွဲ့စည်းထားတယ်လို့ မြင်ရင် (တနည်း နဲ့ အလိုက် integrate လုပ်ရင်) အဲ့ဒီ့အတွဲတွေက force တွေက အတူတူပဲဖြစ်တဲ့အပြင် P ရဲ့ ဆန့်ကျင်ဘက်ကနေ သက်ရောက်တဲ့အတွက် အကုန်ကျေသွားပြီး အမှတ် P မှာ ဘာဆွဲအားမှ မရှိတော့ဘူး။ အလားတူပဲ အမှတ် P ကို တခြားတစ်နေရာပြောင်းပြီ: ဒီအဆင့်တွေအတိုင်း ပြန်တွက်ကြည့်ရင်လည်း Force တွေ အကုန်ကျေသွားတာ တွေ့ရမယ်။ အဲ့ဒါကြောင့် အခေါင်းပေါက်စက်လုံးထဲက ဒြပ်ဆွဲအားဟာ ဘယ်နေရာမှာပဲဖြစ်ဖြစ် သုညပဲရှိတယ်။