Harmonic Oscillator - Part 2

16 May 2018

differential equation harmonic oscillation

ပထမအပိုင်းတုန်းက oscillator ရဲ့ ညီမျှခြင်းဖြစ်တဲ့ $\frac{d^2x}{dt^2}=-x$ ကိုဖြေရှင်းလိုက်တော့ $x=\cos t$ ရခဲ့ပါတယ်။ ဒါပေမယ့်မူလညီမျှခြင်းဖြစ်တဲ့−

\frac{d^2 x}{dt^2}=-\frac{k}{m}  x

ကိုဖြေရှင်းဖို့ကြိုးစားကြည့်ရအောင်။ ဒီညီမျှခြင်းကို ပထမညီမျှခြင်းနဲ့နှိုင်းယှဉ်လိုက်ရင် factor $\frac km$ ပိုလာတယ်ဆိုတော့ အဖြေ $x (= \cos t)$ ကိုတစ်ခုခုနဲ့မြှောက်ရင် အဖြေမှာအဲ့ဒီ factor ပါလာနိုင်မလား။ အရင်ဆုံး $x$ ကို ကိန်းသေ $A$ နဲ့မြှောက်ပြီး $x=A \cos t$ ကိုအစားသွင်းလိုက်ရင် အဖြေက $-Ax$ ရလားကြည့်ရအောင်။

x=A\cos t

\frac{dx}{dt}=-A\sin t

\frac{d^2x}{dt^2}=-A\cos t=-x

အဲ နောက်ဆုံးအဖြေမှာ ကျွန်တော်တို့လိုချင်တဲ့ $x$ ရှေ့က factor A ပါမလာပါဘူး။ ဒီတော့ $x=A\cos t$ က လိုချင်တဲ့အဖြေမဟုတ်သေးပါဘူး။ ဒါပေမယ့် သူက $\frac{d^2x}{dt^2}=-x$ ရဲ့အဖြေဖြစ်နေတာကိုပဲ တွေ့ရပါတယ်။ ဒါကတိုက်ဆိုင်တာမဟုတ်ပဲ LDE တွေရဲ့ဂုဏ်သတ္တိတစ်ခုပဲဖြစ်ပါတယ်။ LDE ရဲ့အဖြေ (LDE ကိုပြေလည်စေသော function) တစ်ခုကို constant တစ်ခုနဲ့မြှောက်ခြင်းကလည်း အဖြေနောက်တစ်ခုပဲဖြစ်ပါတယ်။ တစ်နည်း $x$ က LDE တစ်ခုရဲ့အဖြေဖြစ်မယ်ဆိုရင် $Ax$ ကလည်း သူ့ရဲ့အဖြေပဲဖြစ်တယ်။ အလေးတုံးအခြေအနေနဲ့ပြောရရင် $x$ ကို 2 နဲ့မြှောက်တာက အလေးတုံးသွားတဲ့အကွာအဝေး၊ အရှိန်တွေကိုပါ နှစ်ဆတိုးသွားစေပါတယ်။ ဒါပေမယ့် အကွာအဝေးနှစ်ဆကို အရှိန်နှစ်ဆနဲ့သွားတဲ့အတွက် အချိန်ကအတူတူပဲယူပါတယ်။ တစ်နည်းပြောရရင် $x$ နဲ့ $2x$ က အပေါ်အောက်ရွေ့လျားချိန် time scale (period) မှာအတူတူပဲဖြစ်ပြီ: ရွေ့လျားတဲ့အကွာအဝေး (သို့) လွှဲကျယ် (amplitude) ပဲကွာတာဖြစ်ပါတယ်။

ညီမျှခြင်း (၁) ကိုဖြေရှင်းဖို့ နောက်ကိန်းတစ်ခုကိုတင်သွင်းကြည့်ပါမယ်။ ဖြစ်နိုင်တဲ့ function အမျိုးမျိုးကို ဒီညီမျှခြင်းထဲထည့်ပြီ: ပြေလည်စေလားဆိုတာကြည့်တာပေါ့။ ဒီတော့ $x$ ကို constant နဲ့မြှောက်တာမရဘူးဆိုရင် time variable ဖြစ်တဲ့ $\cos t$ ထဲက $t$ ကိုမြှောက်ကြည့်ရင်ရော။ ဥပမာ $x=\cos \omega_0 t$ က ညီမျှခြင်း (၁) ပုံစံကိုပြေလည်စေလားဆိုတာ စမ်းကြည့်ရအောင်။ $\omega_0$ က စောစောက A လိုပဲ ကိန်းသေတစ်ခုပါပဲ။

x=\cos \omega_0 t

\frac{dx}{dt}=-\omega_0 \sin \omega_0 t

\frac{d^2x}{dt^2}=-\omega_0^2 \cos \omega_0 t

ဒီညီမျှခြင်းကို ညီမျှခြင်း (၁) နဲ့နှိုင်းယှဉ်ကြည့်ပြီး $\omega_0^2 = \frac km$ ကိုထည့်လိုက်ရင် $x=\cos \sqrt{\frac km} t$ က ဒီညီမျှခြင်းကို ပြေလည်စေတာတွေ့ရပါမယ်။ ဒီမှာသုံးတဲ့ $\omega_0$ ကိုယ်တိုင်ကလည်း အရေးပါတဲ့ကိန်းတစ်ခုဖြစ်တဲ့အတွက် နောက်ပိုင်းမှာသူ့ကိုပဲ အသုံးပြုသွားပါမယ်။

$\omega_0$ ကဘာကိုဆိုလိုတာလဲ၊ တစ်နည်း $\omega_0$ ကဘာကိုပြတဲ့ကိန်းလဲ။ $\cos \omega_0 t$ ကိုကြည့်ပါ။ Cosine function ကသိတဲ့အတိုင်း periodic function လို့ခေါ်တဲ့ အဝိုင်းပတ်သလိုပြန်ပြန်ထပ်နေတဲ့ function တစ်ခုဖြစ်တယ်။ သူ့ရဲ့တစ်ပတ်ပြန်လည်တဲ့ထောင့်က $2\pi$ ။ ဒီတော့ $\omega_0 t=2\pi$ မှာ $x$ က မူလတန်ဖိုးပြန်ရောက်မယ် (အလေးတုံးကမူလနေရာပြန်ရောက်မယ်)။ တစ်ပတ်ပြည့်ဖို့ကြာမယ့်အချိန်(period) ကတော့ $t_b=\frac{2\pi}{\omega_0}$ ဖြစ်မယ်။ ဒီတော့ အလေးတုံးထက်အောက်တစ်ပတ်လွှဲချိန် (period) က $\omega_0$ နဲ့ပြောင်းပြန်အချိုးကျပါတယ်။ $\omega_0$ ညီမျှခြင်းကို နောက်တစ်ခေါက်ပြန်ကြည့်စို့။

\omega_0 = \sqrt{\frac km}

t_b=\frac{2\pi}{\omega_0}=2\pi \sqrt{\frac mk}

ဒီညီမျှခြင်းအရ period က အလေးတုံးဒြပ်ထု (m) နဲ့တိုက်ရိုက်အချိုးကျပြီ: စပရိန်ကိန်းသေ (k) နဲ့ပြောင်းပြန်အချိုးကျပါတယ်။ ပိုလေးတဲ့အလေးတုံးကိုသုံးရင် အင်နားရှားများတဲ့အတွက် လှုပ်ရှားမှုနှေးပြီးအိပဲ့အိပဲ့ဖြစ်နေတာကြောင့် တစ်ပတ်ပြည့်ဖို့အချိန်ပိုယူပါတယ်။ စပိရိန်ကိန်းသေများတာကိုသုံးရင် စပရိန်ကပိုတောင့်တာကြောင့် အလေးတုံးကိုပိုဆွဲနိုင်ပြီး မြန်မြန်လှုပ်ရှားစေတာဖြစ်ပါတယ်။

$\omega_0$ ကို spring-mass စနစ်ရဲ့ သဘာဝကြိမ်နှုန်း (natural frequency) လို့ခေါ်ပါတယ်။ အခုလောလောဆယ် ဒီစနစ်ကပြင်ပသက်ရောက်အားမရှိပဲ သူ့သဘာဝအတိုင်းလှုပ်ရှားနေတာကြောင့် ဒီလိုခေါ်တာဖြစ်ပါတယ်။ ကြိမ်နှုန်း (frequency) ဆိုတာ တစ်စက္ကန့်အတွင်း အလေးတုံး အပေါ်အောက်ဘယ်နှစ်ပတ်ရွေ့လဲဆိုတာပြတဲ့ကိန်းပါ။ Period အတိုင်းပဲ natural frequency ကလဲ ဒီစနစ်ကိုဖွဲ့စည်းထားတဲ့ spring constant နဲ့ mass တို့ပေါ်မူတည်ပါတယ်။

$k$ နဲ့ $m$ ကိုသိရင် $t_b$ နဲ့ $\omega_0$ ကိုတွက်လို့ရပါတယ်။ ဒါပေမယ့် ဘယ်လောက်ရွေ့မယ် ( $x_max$ )၊ တစ်နည်း လွှဲကျယ်(amplitude) ကိုတော့ တွက်လို့မရသေးပါဘူး။ Amplitude ကအလေးတုံးကို စတင်လှုပ်ရှားစေတဲ့အခြေအနေ (initial $x$ or velocity $v=\frac{dx}{dt}$ ) ပေါ်မူတည်ပါတယ်။

မူလအခြေအနေများ (Initial conditions)

မူလအခြေအနေဆိုတာ စနစ်ကိုစတင်တွက်ချက်တဲ့အချိန် ( $t=0$ ) မှာရှိတဲ့ အရွေ့ ( $x$ နဲ့ အလျင် $v$ ) တန်ဖိုးတွေပဲဖြစ်ပါတယ်။ အပေါ်မှာပြောခဲ့တဲ့အတိုင်း အလေးတုံးရဲ့လွှဲကျယ်(amplitude) က $t=0$ မှာရှိတဲ့ $x$ နဲ့ $v$ တို့ပေါ်မူတည်ပါတယ်။ Natural frequency ကိုချုပ်ကိုင်ထားတဲ့ spring constant နဲ့ mass ကိုမပြောင်းလဲသရွေ့ frequency နဲ့ အပေါ်အောက်တစ်ပတ်ပြည့်ဖို့ကြာချိန် (period) ကပြောင်းလဲမှာမဟုတ်ပါဘူး။ ဒီသဘောတရားကို LDE ညီမျှခြင်းကဘယ်လိုပြောပြနေလဲဆိုတာ လေ့လာဖို့ ညီမျှခြင်း(၁) ရဲ့ အဖြေတစ်ခုဖြစ်တဲ့ $x=A \cos \omega_0 t$ ကိုကြည့်ပါ။ $A$ က maximum amplitude ကိုပြတာဖြစ်ပြီး သူ့ရဲ့တန်ဖိုးက initial displacement $x(0)$ ပေါ်မူတည်ပါတယ်။

အောက်မှာ harmonic oscillator ကိုသရုပ်ပြတဲ့ app တစ်ခုရှိပါတယ်။ mass, spring constant နဲ့ initial x တို့ကိုပြောင်းလဲပြီးစမ်းကြည့်ပါ။ လှုပ်ရှားစေဖို့ Run ကိုနှိပ်ပါ။ Geogebra applet credit : Harmonic oscillator

Simple Harmonic Motion Simulation

အောက်မှာ အလေးတုံးရဲ့ position ကို time အလိုက်နမူနာဂရပ်(အပြာရောင်) ဆွဲထားပါတယ်။ အပေါ်မှာရခဲ့တဲ့အဖြေအတိုင်း amplitude က $A$ နဲ့ period က $t_b$ ဖြစ်ပြီ: ဂရပ်က cosine function ပုံဖြစ်ပါတယ်။

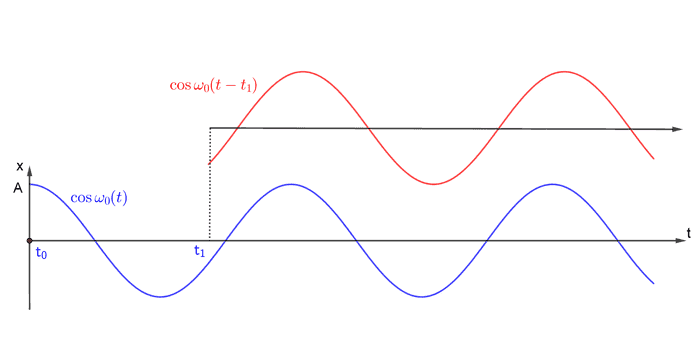
ဒီဂရပ်က မူလအခြေအနေမှာ position $A$ မှာရှိနေတဲ့ အလေးတုံးရဲ့ရွေ့လျားမှုပုံစံဖြစ်ပါတယ်။ ဒါပေမယ့် ဒီ spring-mass စနစ်က အခန်းတစ်ခုထဲမှာရှိနေပြီး သင်ကအချိန် $t_1$ ကျမှအခန်းတံခါးကိုဖွင့်ကြည့်လိုက်တယ်ဆိုပါတော့။ သင့်ညီမျှခြင်းတွေအတွက် $t_1$ မှာရှိနေတဲ့ အလေးတုံးရဲ့ position နဲ့ velocity တွေက initial condition တွေဖြစ်နေပါမယ် (တစ်နည်း $t_1$ က သင့်အတွက် $t_0$ ဖြစ်နေပြီး time scale က $t_1$ ပမာဏရွေ့သွားပါတယ်)။ အနီရောင်ဂရပ်နဲ့ပြထားတဲ့ ဒီအခြေအနေအတွက် ညီမျှခြင်း(၁) ရဲ့ နောက်အဖြေတစ်ခုက $x=A \cos \omega_0 (t-t_1)$ ဖြစ်ပါတယ်။ $t_1$ က ကိန်းသေဖြစ်တဲ့အတွက် $\omega_0 t_1$ ကို $\Delta$ လို့ခေါ်မယ်ဆိုရင်−

x(t)=A \cos (\omega_0 t+\Delta)

x(t)=A (\cos \omega_0 t \cos \Delta - \sin \omega_0 t \sin \Delta)

x(t)=A' \cos \omega_0 t+ B' \sin \omega_0 t

where

A'=A \cos \Delta \text{ and } B'=B \cos \Delta

$A'$ နဲ့ $B'$ က initial condition တွေကနေရှာရမှာဖြစ်ပါတယ်။ ဒီအဖြေက ညီမျှခြင်း (၁)ရဲ့ ယေဘူကျအကျဆုံးအဖြေဖြစ်ပါတယ်။